A note on ALS failure

The first time we ran the tests for the Section A Second Random Example of the 2 to the 9th tensors, we used the ALS algorithm at fixed rank rather than growing the rank (see ALS Performance Notes). The fixed-rank algorithm performed much worse. In the following table we give the corresponding visualizations produced by the two algorithms.

Rank	Fixed Rank	Growing Rank
16
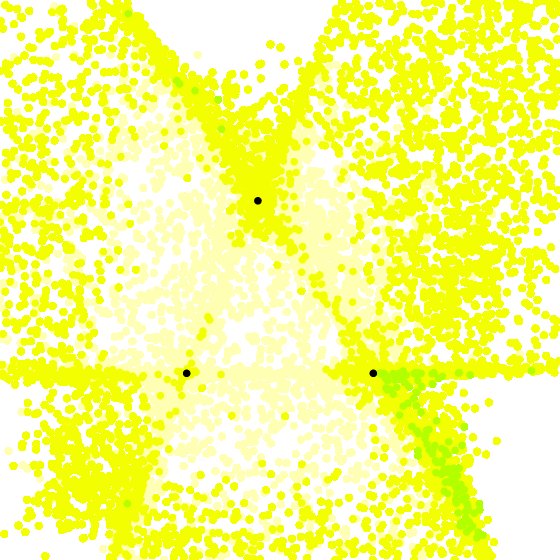
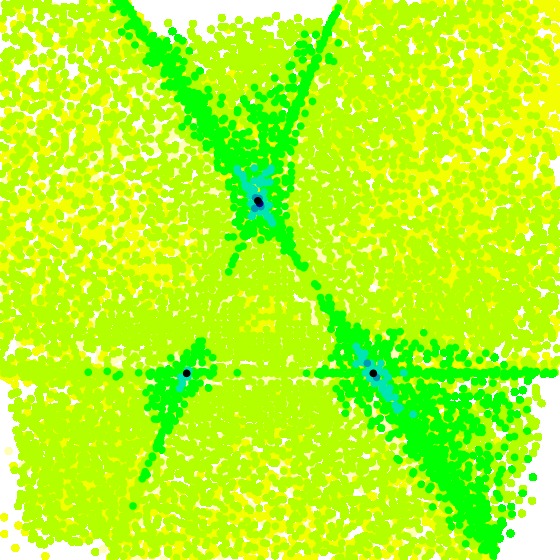
32
40
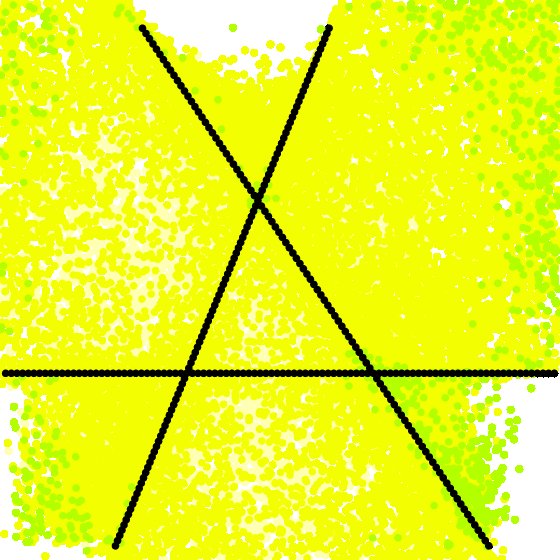
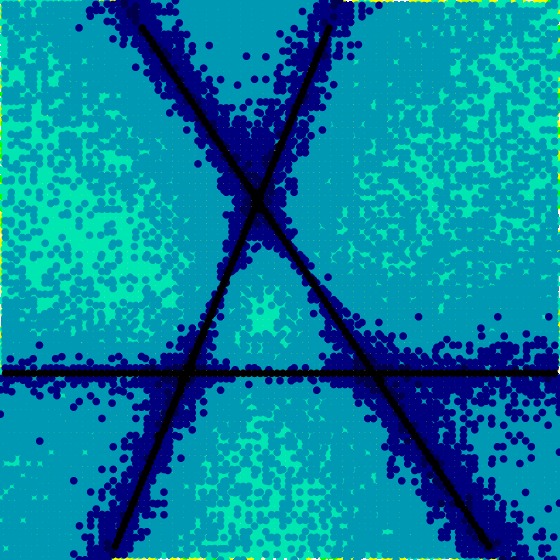
48

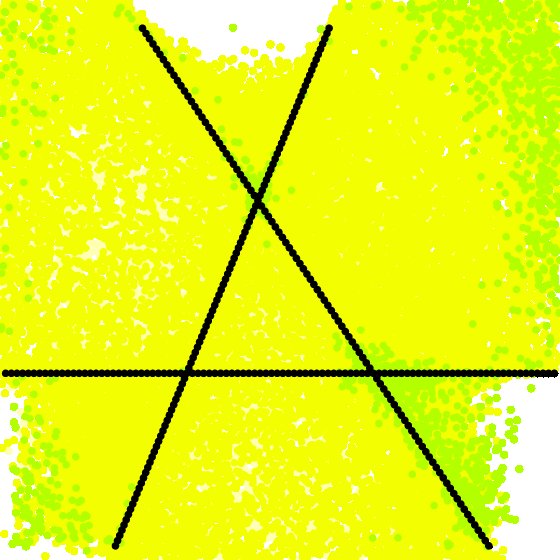
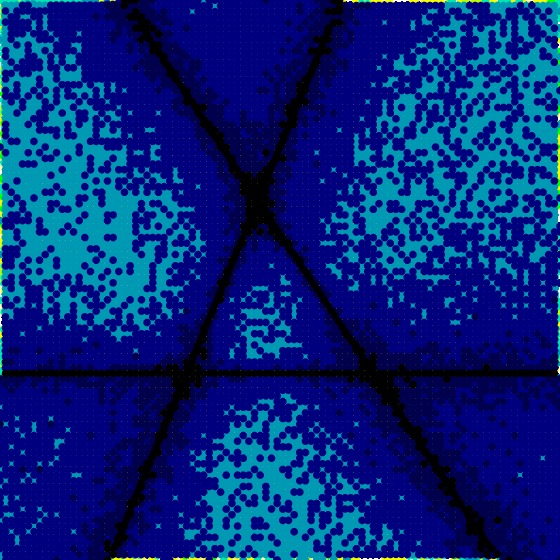
Zoomed out to the square \([-2,3]\times[-2,3]\), the fixed-rank visualization of \(S_{48}\) gives

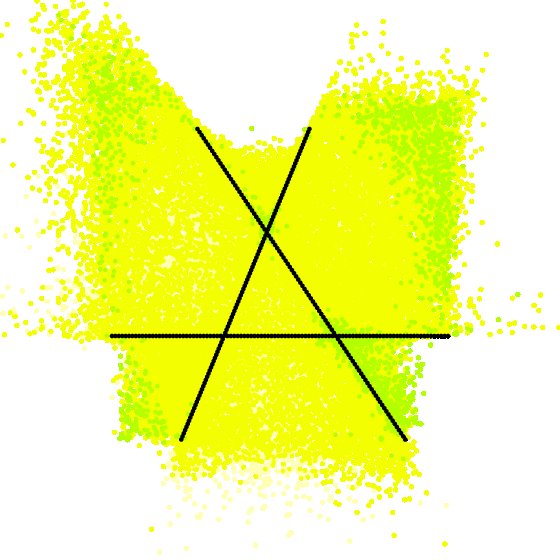
Since the ALS routine was called for a grid of tensors in \([-1,2]\times[-1,2]\), the points outside this region indicate that the fixed-rank ALS sometimes found the ‘best’ approximation to be quite far from the target tensor in terms of its projection as well as its angle.