3 by 3 by 3 Tensors¶
We now study the case of 
tensors over the
real and complex numbers. Our goals are
- to determine the maximum separation rank
of such tensors and - to explore the geometry of
for some less than
the maximum.
In principle one can never determine the maximum separation rank
using a numerical routine such as this, since one could be
unlucky and miss it. Generally one can only hope to determine the
typical separation rank.
Visualizations over the Real numbers¶
In [KRUSKA1989], Kruskal claims to have shown rank 
,
but his results were not published. Jos ten Berge says that he saw
this 20 page proof but discarded it when Roberto Rocci
provided a 4 page proof in 1993, which is also unpublished but is available.
A full proof is published in [BRE-HU2013].
A Random Example¶
We choose 
, 
, and 
randomly in
. Since these three tensors are in , any tensor
on the line connecting any two of them is in 
, and a tensor
in the plane is generically in 
, which we suppose is large
enough to capture general tensors.
We first produce a visualization of 
on
![[-1,2]\times[-1,2]](_images/math/ea61045a4371f2a1c81de0708a04d9b9278331ec.png)
, and obtain
[data file 3x3x3pr4random.dat]
There are only a few scattered black points. Thus we conclude that the
maximum separation rank of a tensor over
the real numbers is more than 4.
Next, using the same set of random , , and
, we produce a visualization of 
, and obtain
[data file 3x3x3pr5random.dat] Black points are distributed over the whole plane, with no apparent voids. We interpret this as validating the result that the maximum rank is 5.
Finally, using the same set of random , , and
, we first produce a visualization for ,
expecting it to be solid black. Since the line connecting any two
is in , these lines appear in the
visualization, and help to locate the . We obtain the
visualization
[data file 3x3x3pr6random.dat]
The occasional lighter point is attributed to failure in the routine
that tries to fit a tensor on the plane with a tensor in .
A Specific Example¶
We now consider a specific example that was suggested as possibly interesting. The target tensor, which has nominal rank 5, is
![X_5 &= [1,0,0]\otimes[1,0,0]\otimes[1,0,0]
+[1,0,0]\otimes[0,0,1]\otimes[0,0,1]\\
&+[0,1,0]\otimes[1,0,0]\otimes[0,1,0]
+[0,1,0]\otimes[0,1,0]\otimes[0,0,1]\\
&+[0,0,1]\otimes[1,0,0]\otimes[0,0,1]
\,,](_images/math/cf918148fb870b62a7cb063d7690ded8c41e5d94.png)
which can also be viewed as
![X_5 = [1,0,0]\otimes\left[\begin{array}{ccc}
1&0&0\\0&0&0\\0&0&1\end{array}\right]
+ [0,1,0]\otimes\left[\begin{array}{ccc}
0&1&0\\0&0&1\\0&0&0\end{array}\right]
+ [0,0,1]\otimes\left[\begin{array}{ccc}
0&0&1\\0&0&0\\0&0&0\end{array}\right]
\,.](_images/math/17f59eec1f194de4f8d89aa3f26196cb91e89daf.png)
Using the plane defined by the three tensors
![T_1&= [1,0,0]\otimes[1,0,0]\otimes[1,0,0]
+[1,0,0]\otimes[0,0,1]\otimes[0,0,1]\\
T_2&= [0,1,0]\otimes[1,0,0]\otimes[0,1,0]
+[0,1,0]\otimes[0,1,0]\otimes[0,0,1]
\quad\text{and}\\
T_3&= [0,0,1]\otimes[1,0,0]\otimes[0,0,1]
\,,](_images/math/60228bfe2a51444b21ddb82e68d7cf48515993a1.png)
the point 
is in their center.
We first produce a visualization of on
, and obtain
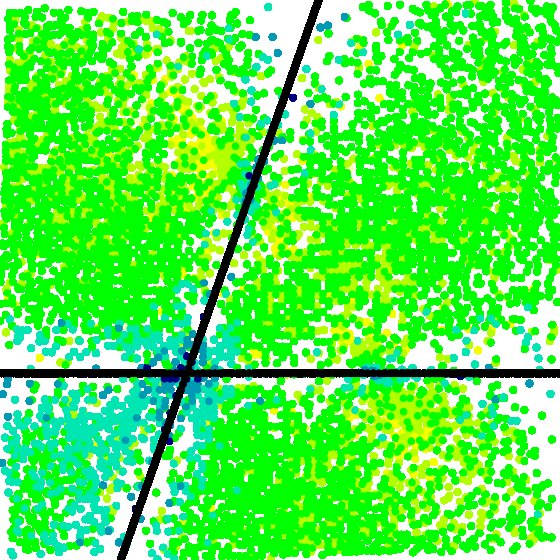
[data file 3x3x3pr3X5.dat]
Since the region in the vicinity of has no black points,
we conclude it is not rank 3. We next produce a visualization of
and obtain
[data file 3x3x3pr4X5.dat]
A large number of test points were needed to produce this
visualization. We used more points near the center to try to get
better resolution there. Although there are not that many black
points, they are spread throughout the visualization with no apparent
voids. We also tried zooming in on a relatively light region near the
center and adding many more points there, and were then able to find
dark points. Based on this behavior, we conclude that is
probably of rank 5 but reachable as a limit of rank 4 tensors.
Visualizations over the Complex numbers¶
The rank over the complex numbers is at most the rank over the real
numbers, so we now investigate whether or not the maximum rank is
strictly smaller for tensors.
A Random Example¶
We choose and randomly in , so that
a tensor in the plane is generically in , which we know is
large enough to capture general tensors.
We then produce a visualization of and obtain
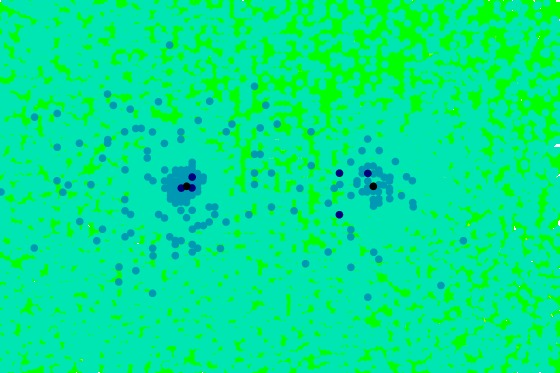
[data file 3x3x3pr4randomC.dat]
Since there are few black points, we conclude the maximum rank over
the complex numbers is more than 4, and hence is 5. As an additional
check, we use the same and and produce a
visualization of , and obtain
[data file 3x3x3pr5randomC.dat]
A Specific Example¶
We now reconsider the tensor , which we studied in the real
case. We use the complex line defined by
![T_1&= [1,0,0]\otimes[1,0,0]\otimes[1,0,0]
+[1,0,0]\otimes[0,0,1]\otimes[0,0,1]\quad\text{and}\\
T_2&= [0,1,0]\otimes[1,0,0]\otimes[0,1,0]
+[0,1,0]\otimes[0,1,0]\otimes[0,0,1]
+[0,0,1]\otimes[1,0,0]\otimes[0,0,1]
\,.](_images/math/14059e011024f2845479d1a68e89ed052c5f9c7d.png)
We first produce a visualization of on
![[-1,2]\times[-i,i]](_images/math/0a230449fd788d33298d0df771f7e780ac02f5c0.png)
, and obtain
[data file 3x3x3pr3X5C.dat]
Since there are essentially no black points, we then produce a
visualization of and obtain
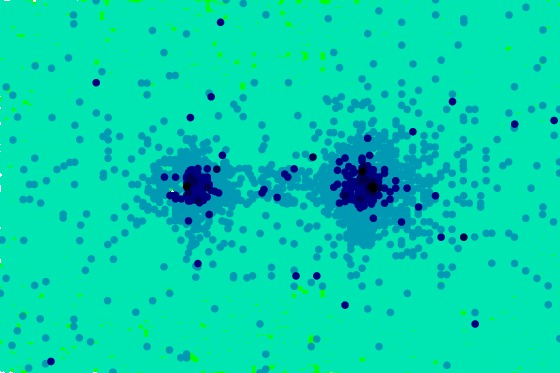
[data file 3x3x3pr4X5C.dat]
This visualization required quite a lot of points and effort. The
scattered dark blue points indicate that rank 4 points are present (or
nearby) but that they are hard to construct. We zoomed in to
![[0.4,0.6]\times[-0.1i,0.1i]](_images/math/ee183add798f27de2edc73c09d2c5ee3d5f15d46.png)
and added points near ,
and obtain
Based on this behavior, we again conclude that is probably
of rank 5 but reachable as a limit of rank 4 tensors.